Integral Identities

Formal Integral Definition:
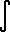
f(x) dx = lim _{(d -> 0)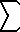} (k=1..n) f(X_(k)) (x_(k) - x_(k-1)) when...

a = x₀ < x₁ < x₂ < ... < x_n = b

d = max (x₁-x₀, x₂-x₁, ... , x_n - x_(n-1))

x_(k-1) <= X_(k) <= x_(k)     k = 1, 2, ... , n

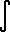
F '(x) dx = F(b) - F(a) (Fundamental Theorem for integrals of derivatives)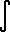

---

a f(x) dx = a 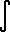f(x) dx (if a is constant) 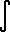f(x) + g(x) dx = 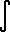f(x) dx + 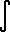g(x) dx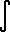
f(x) dx = 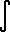f(x) dx | (a b)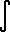
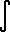
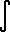
f(x) dx + f(x) dx = f(x) dx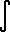
f(u) du/dx dx = 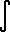f(u) du (integration by substitution)